Об алгоритме
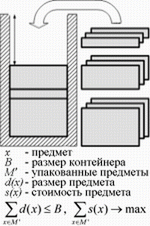 Всякий раз, когда требуется разместить товары на складе или загрузить их в транспортное средство, мы сталкиваемся с проблемой сложить груз так, чтобы он занимал как можно меньше места, или, иными словами, с задачей об оптимальной упаковке. Ученые называют ее «Задачей о рюкзаке».
Всякий раз, когда требуется разместить товары на складе или загрузить их в транспортное средство, мы сталкиваемся с проблемой сложить груз так, чтобы он занимал как можно меньше места, или, иными словами, с задачей об оптимальной упаковке. Ученые называют ее «Задачей о рюкзаке».
В математической литературе чаще встречается одномерный вариант задачи об упаковке. Было установлено, что эта задача является NP-полной. При постановке задачи об упаковке в трехмерном пространстве, она будет заведомо сложнее одномерной, но по-прежнему может быть решена за полиномиальное время на недетерминированных вычислительных устройствах. Следовательно, трехмерная задача об упаковке является NP-полной.
К сожалению, все известные алгоритмы, решающие какую-нибудь из NP-полных задач и, в частности, задачу об упаковке, имеют экспоненциальную временную сложность, что эквивалентно полному перебору всех возможных вариантов. Это означает, что даже при небольшом количестве грузов (около 50) время работы программы, реализующей такие алгоритмы, будет измеряться годами даже при использовании современных суперкомпьютеров. Недаром в 2000 году Математический институт Клэя, входящий в состав Кембриджа, включил задачу нахождение быстрого (полиномиального) алгоритма для решения переборных задач в список из 7 задач, предложив за решение каждой из них премию в 1 млн. долларов!
Выходом из этой ситуации является создание приближенных эвристических алгоритмов, которые за приемлемое время находят решение, близкое к оптимальному.

В основу используемых нами алгоритмов в программе packer3d и online сервисе по расчету оптимального плана загрузки разнотипных грузов положены теоретические и прикладные исследования, которые были начаты на кафедре МАТИС механико-математического факультета Московского государственного университета им. М.В. Ломоносова в 2000 году под руководством к.ф.-м.н. А.С. Строгалова и к.ф.-м.н. А.А. Ирматова. Результатом этих исследований стали уникальные эвристические алгоритмы с элементами нейросетевых и генетических вычислений, созданные на стыке дискретной математики, математической логики и математической статистики. Мы продолжаем сотрудничать с кафедрой МАТИС МГУ в области развития существующих и создания новых алгоритмов в логистике и других сферах.
Плотность заполнения в результате работы этого алгоритма составляет в среднем 80-95% от объема грузового отсека, а время работы для сотен ящиков - несколько минут. При расчете могут быть учтены различные дополнительные ограничения, такие как грузоподъемность, максимальное давление на ящик, сбалансированность давления на оси, штабелирование, паллетизация и многие другие. Кроме того, можно выбрать один из трех вариантов загрузки: через заднюю дверь, как в фургон или контенейнер, через боковую дверь, как в вагон, или сверху вниз, как на платформу.
Подробнее с математическими методами, лежащими в основе packer3d можно ознакомиться на странице Наша научная работа.